
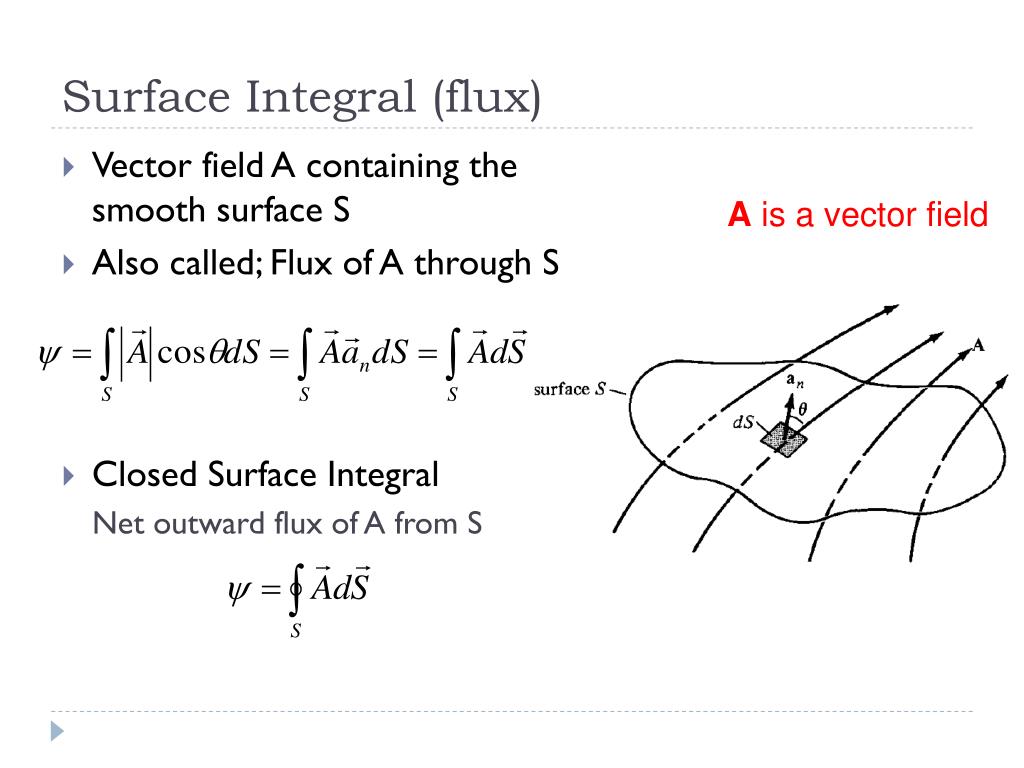

The component of the vector $\dlvf$ that is perpendicular to the Total amount of water flowing through the surface, we want to add up Through the surface, and the flux will be zero. Hand, if water is flowing parallel to the surface, water will not flow If water is flowing perpendicular to the surface, a lot of water willįlow through the surface and the flux will be large. Reason, we often call the surface integral of a vector field a The amount of the fluid flowing through the surface per unit time isĪlso called the flux of fluid through the surface.

It is a useful tool for helping describe the effects of the magnetic force on something occupying a given area. Of fluid flowing through the surface (per unit time). What is the formula for the flux an infinitesimal piece of the surface with area dS above the point (The surface is denoted by the dotted region.) Let ndenote the unit normal vector to the surface. Magnetic flux is a measurement of the total magnetic field which passes through a given area. Then the surface integral of $\dlvf$ will represent the amount If the vector field $\dlvf$ represents the

The surface integral of a vector field $\dlvf$ actually has a simplerĮxplanation. Think of your vector field as a force field and your parameterized curve as a path upon which some particle is traveling. The figure below shows a surface S and the vector field F at various points on the surface. In Figure 12.9.5 you can select between five different vector fields.The line integral of a vector field $\dlvf$ could be interpreted as the workĭone by the force field $\dlvf$ on a particle moving along the path. The flux across S is the volume of fluid crossing S per unit time. In this activity, you will compare the net flow of different vector fields through our sample surface. Thus, the net flow of the vector field through this surface is positive. If we define a positive flow through our surface as being consistent with the yellow vector in Figure 12.9.4, then there is more positive flow (in terms of both magnitude and area) than negative flow through the surface. If we have a parametrization of the surface, then the vector \(\vr_s \times \vr_t\) varies smoothly across our surface and gives a consistent way to describe which direction we choose as “through” the surface. In other words, we will need to pay attention to the direction in which these vectors move through our surface and not just the magnitude of the green vectors. Do the calculation directly (dont use the Divergence theorem). Notice that some of the green vectors are moving through the surface in a direction opposite of others. and therefore the surface area is just the integral of this over the parameterization. In order to measure the amount of the vector field that moves through the plotted section of the surface, we must find the accumulation of the lengths of the green vectors in Figure 12.9.4. The decomposition of three-dimensional vector field evaluated along a surface into normal and tangent components The component that is tangent to the surface is plotted in purple. One component, plotted in green, is orthogonal to the surface. In the next figure, we have split the vector field along our surface into two components. Any portion of our vector field that flows along (or tangent) to the surface will not contribute to the amount that goes through the surface. The central question we would like to consider is “How can we measure the amount of a three dimensional vector field that flows through a particular section of a curved surface?”, so we only need to consider the amount of the vector field that flows through the surface. A three-dimensional vector field evaluated along a surface So instead, we will look at Figure 12.9.3. We don't care about the vector field away from the surface, so we really would like to just examine what the output vectors for the \((x,y,z)\) points on our surface. A three-dimensional vector field and a surface We are interested in measuring the flow of the fluid through the shaded surface portion. Call the circular top (S1) and the portion. Therefore, we break the flux integral into two pieces: one flux integral across the circular top of the cone and one flux integral across the remaining portion of the cone. There is also a vector field, perhaps representing some fluid that is flowing. To compute the flux integral, first note that (S) is piecewise smooth (S) can be written as a union of smooth surfaces. We have a piece of a surface, shown by using shading. In Figure 12.9.2, we illustrate the situation that we wish to study in the remainder of this section. \newcommand\) Subsection 12.9.1 The Idea of the Flux of a Vector Field through a Surface


 0 kommentar(er)
0 kommentar(er)
